Who wants to be a millionaire?
If you’ve come for advice on how to become rich, I’m sorry but you’ve come to the worst possible finance article of all time. You’ve once again been the victim of click-bait.
However, this article does talk about one of the possible (probably the hardest) ways to earning that one million. The Clay Mathematics Institute offers a prize of $1,000,000 for the first correct solution of any one of its seven Millennium Prize Problems. One of its seven problems, and probably the easiest to explain, is the P vs. NP problem.
The question –
Given a problem whose solution can be checked in polynomial time, is it possible to solve it in polynomial time?
Let us consider the problem of sorting an array of numbers. There are several algorithms which can sort in n log n time, thus making it a p-problem.
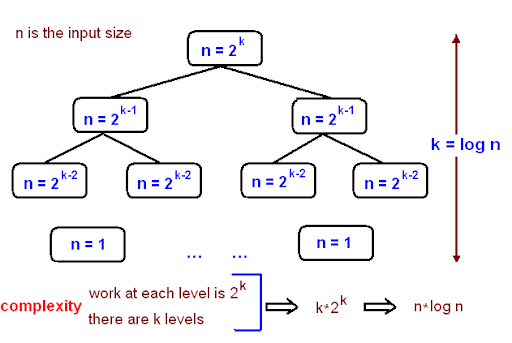
Now, consider a 9 x 9 Sudoku puzzle. A really, really hard 9 x 9 puzzle. You might not be able to solve it in a reasonable (polynomial) amount of time, but don’t worry, neither can a computer! However, once you’ve checked the answer from the back of the book, it is easy for you to verify its correctness. (polynomial time)
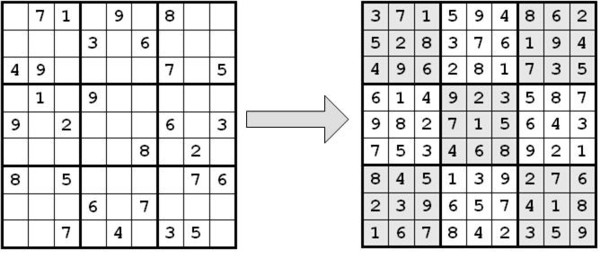
Therefore, the million-dollar question (literally) is – is the ability to recognize the correctness of a solution in polynomial time enough to find a polynomial-time solution?
Why is this important?
Perhaps you aren’t a great Sudoku fan (well, neither am I). So, why is it important for people like us?
Banks (actually, most of modern cryptography) rely on the fact that integer factorisation is an NP problem. This basically means that a polynomial solution to a Sudoku problem directly implies the existence of a possible polynomial solution to break encryption. A “easy” solution to Sudoku would make protein-folding easier, essentially beating cancer!
Understanding NP
NP stands for Non-deterministic Polynomial time. NP represents the class of problems whose solutions can be verified in a polynomial amount of time. Note that every P problem is also NP, because one way of checking a solution is to calculate the solution yourself. If finding the solution takes polynomial time, checking will also take polynomial time in the worst case.
How do Sudoku and solving cancer have anything in common? Well, scientists have discovered that a lot of NP problems are essentially the same problem with a little polynomial adjustments to be done here and there. To solve the problem of P vs. NP, the concept of NP-complete might come in handy.
NP-complete problems are a set of problems to each of which any other NP-problem can be reduced in polynomial time, and whose solution may still be verified in polynomial time. Therefore, since every problem in NP-complete is essentially the same, solving one problem in P time would lead to a solution to every other problem in NP-complete, thus solving P = NP. This is what trivial games like Sudoku and Super Mario have in common with complex computational problems like the Travelling Salesman etc. They all share the same solution.
Are there only two classes of problems?
There exist many other classes such as EXPTIME where even verifying a solution takes a lot of time. Consider the game of chess as an example. Given a position, what is the best possible next move? Not only is it hard to find, but it is also hard to verify if a move is the best one. While this is good news for Chess players, it opens up the field of computational problems to a much wider “zoo” of complexity classes which includes P, NP, NP-Complete, EXPTIME, Co-NP, PSPACE etc.

Final Thoughts
What would be the implications of P = NP? Apart from the computational benefits, it has major consequences. Banking would fall, stock markets would be weak-form efficient, meaning current prices fully reflect all information available in past prices. Philosophically, it would mean that there is no difference from finding the solution and understanding it. Scott Aaranson, a complexity researcher at MIT, put it best:
“If P=NP, then the world would be a profoundly different place than we usually assume it to be. There would be no special value in “creative leaps,” no fundamental gap between solving a problem and recognising the solution once it’s found. Everyone who could appreciate a symphony would be Mozart; everyone who could follow a step-by-step argument would be Gauss; everyone who could recognise a good investment strategy would be Warren Buffett”
Author,
Madhumitha Nara,
2nd Year, IT,
NITK



